Indy's Astronomy Glossary
Finding Your Way in the Cosmos
Finding Your Way in the Cosmos
Right Ascension (RA) is similar to longitude on the Earth, however it is numbered differently.
Longitude starts at 0 degrees at the Prime Meridian and goes to 180 degrees
West or 180 degrees East. Since the Earth is a sphere, 180 West is equal
to 180 East. Right Ascension, on the other hand, is measured in hours instead of degrees.
It starts at 0 hours at the First Point of Aries and goes all the way around the inside
of the celestial sphere to 24 hours which is at the same place as 0 hours. A star that has an
RA of 12 hours is on the opposite side of the sky from one that is at 0 hours.
Once you know a star's RA, you can use Local Sidereal Time
to predict when it will be in line with your local meridian.
Declination (Dec) is very much like latitude on the Earth. A Dec of 0 degrees points to the "Celestial Equator" just like a latitude of 0 is at the Earth's Equator. Similarly, a Dec of +90 degrees points to the "North Celestial Pole" and -90 degrees points to the "South Celestial Pole." In this case, the word Celestial is used to distinguish between the North Pole in the sky and the North Pole on the Earth. The Celestial Poles lie directly above the Poles on the Earth, so if you were at the North Pole, the North Celestial Pole would be directly overhead. Stars or constellations with a large negative declination appear only in the Southern sky, and stars or constellations with a large positive declination appear only in the Northern sky.
Always keep in mind when navigating around the Celestial Sphere, that RA and Dec are directions, and not three dimensional positions. RA and Dec do not specify the distance in light years from earth, just the observed direction on the two dimensional surface of the "sphere" from our viewpoint.
The stars on the celestial sphere appear fixed in position for all practical purposes, and because they are very far away their apparent direction is not significantly affected by the orbit of the earth around the sun. Still, the RA and Dec co-ordinates do not stay the same over a long period of time. The main reason co-ordinates change is because of precession. Another reason co-ordinates change is because of proper motion.
Declination (Dec) is very much like latitude on the Earth. A Dec of 0 degrees points to the "Celestial Equator" just like a latitude of 0 is at the Earth's Equator. Similarly, a Dec of +90 degrees points to the "North Celestial Pole" and -90 degrees points to the "South Celestial Pole." In this case, the word Celestial is used to distinguish between the North Pole in the sky and the North Pole on the Earth. The Celestial Poles lie directly above the Poles on the Earth, so if you were at the North Pole, the North Celestial Pole would be directly overhead. Stars or constellations with a large negative declination appear only in the Southern sky, and stars or constellations with a large positive declination appear only in the Northern sky.
Always keep in mind when navigating around the Celestial Sphere, that RA and Dec are directions, and not three dimensional positions. RA and Dec do not specify the distance in light years from earth, just the observed direction on the two dimensional surface of the "sphere" from our viewpoint.
The stars on the celestial sphere appear fixed in position for all practical purposes, and because they are very far away their apparent direction is not significantly affected by the orbit of the earth around the sun. Still, the RA and Dec co-ordinates do not stay the same over a long period of time. The main reason co-ordinates change is because of precession. Another reason co-ordinates change is because of proper motion.
Precession is a slow circular shift of the Earth's orientation in space with respect
to the rest of the galaxy caused by a very regular wobble in the earths
axis. Precession does not change the tilt or angle significantly, just
the direction of the axis. It is much the same as the way the axis of a
spinning top wobbles around in a circle. That also is precession, but on
a much smaller scale.
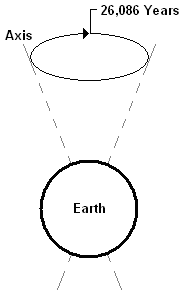
Around 3000 BC (5,000 years ago) the star Thuban in the constellation Draco was the north star. Today, the north celestial pole is located very close to Polaris, the end star in the handle of the little dipper (Ursa Minor). This change is because the wobble in the Earth's axis causes the north
celestial pole to move in a loop around the north ecliptic pole every 26,086
years, ending up back where it started. This movement of the celestial
pole drags the whole celestial-coordinate system along with it, changing
the whole grid of declination and right ascension.
The vernal equinox at Aries 0° (the so-called, "First Point of Aries") really was in Aries when it was named around 0 A.D., but because of the slow shift in the orientation of the Earth's axis with respect to the rest of the galaxy, the first day of spring has since crept into the stars of Pisces. With right ascension and declination continually changing because of precession, in about 12,000 years Vega will become the north star, and Orion will be a summer constellation instead of a winter occurrence.
Although the background of stars will be changing acording to the season of the year, precession will not affect our calendar seasons. We have leap-years because seasons and astronomical events do not repeat in a whole number of days. A calendar that had the same number of days in each year would, over time, drift with respect to the seasons and astronomical events such as the vernal equinox. By occasionally inserting an additional day into the year, the drift can be corrected. Our calendar, with leap-year adjustment, is tied to the seasons and the vernal equinox, so we see no seasonal drift year on year. Noon on March 21 will always be synchronized with the astronomical first day of spring, no matter what stars are visible at night. The Northern Hemisphere won't be having winter in June or summer in December in 13,000 years.
To account for precession and fix a star's direction on the celestial sphere correctly in both time and location, you need to specify the date for which a right ascension and declination apply. The current standard is equinox 2000.0, which means right ascension and declination at the moment the year 2000 begins. Sometimes this is noted as J2000 or Juxtaposition 2000. When right ascension and declination are given in books and atlases, they should be accompanied with a year date such as 1950 or 2000, indicating the year for which the direction is exactly correct.
The good news is that the amount of change due to precession is usually so slight that it is hardly noticeable in the span of 50 years or so, and even then is mostly noticeable only near the celestial equator. The amount of change in the position of the Earth's axis is about 0.0138° per year, or about 0.7° in 50 years.
The vernal equinox at Aries 0° (the so-called, "First Point of Aries") really was in Aries when it was named around 0 A.D., but because of the slow shift in the orientation of the Earth's axis with respect to the rest of the galaxy, the first day of spring has since crept into the stars of Pisces. With right ascension and declination continually changing because of precession, in about 12,000 years Vega will become the north star, and Orion will be a summer constellation instead of a winter occurrence.
Although the background of stars will be changing acording to the season of the year, precession will not affect our calendar seasons. We have leap-years because seasons and astronomical events do not repeat in a whole number of days. A calendar that had the same number of days in each year would, over time, drift with respect to the seasons and astronomical events such as the vernal equinox. By occasionally inserting an additional day into the year, the drift can be corrected. Our calendar, with leap-year adjustment, is tied to the seasons and the vernal equinox, so we see no seasonal drift year on year. Noon on March 21 will always be synchronized with the astronomical first day of spring, no matter what stars are visible at night. The Northern Hemisphere won't be having winter in June or summer in December in 13,000 years.
To account for precession and fix a star's direction on the celestial sphere correctly in both time and location, you need to specify the date for which a right ascension and declination apply. The current standard is equinox 2000.0, which means right ascension and declination at the moment the year 2000 begins. Sometimes this is noted as J2000 or Juxtaposition 2000. When right ascension and declination are given in books and atlases, they should be accompanied with a year date such as 1950 or 2000, indicating the year for which the direction is exactly correct.
The good news is that the amount of change due to precession is usually so slight that it is hardly noticeable in the span of 50 years or so, and even then is mostly noticeable only near the celestial equator. The amount of change in the position of the Earth's axis is about 0.0138° per year, or about 0.7° in 50 years.
Proper Motion is the apparent change of position of an individual star on the celestial
sphere due to the drift caused by the stars observed speed of movement
and angular motion on the sphere. For most stars, this amount of drift
is very slight and not very obvious in the span of a human lifetime, or
even over 10 generations. While the stars appear generally fixed in position,
like the Sun they are each moving in their own orbit in our galaxy, much
the same as the continents drift imperceptibly on the face of our planet.
From our viewpoint on earth, the stars we see are all wandering around
very slowly in different directions on the celestial sphere. Over the course
of a 100,000 years, the stars will eventually drift far enough so that
the familiar constellations as we know them will eventually be replaced
with completely different patterns.
The apparent motions of the stars in the night sky are caused by the earth's rotation and orbit around the Sun, and the tiny effects of precession, and not related to proper motion. While the proper motion of a star is also an apparent motion, it is the result of the star's own motion in space. Proper Motion is simply a measure of how quickly a star appears to move in the sky based on it's own motion in space.
The observed speed of a stars Proper Motion is usually noted in units of arc seconds per year. A better way is to note arc seconds per year, for both Proper Motion RA and Proper Motion Dec., to define both the observed speed and the observed direction of drift on the celestial sphere . In this case be sure to note if the values are positive or negative. With this information, provided that you also account for precession, you can calculate a stars RA and Dec. over a period of years to determine the direction where the star would appear on the celestial sphere on any given date past or future.
Proper Motion RA and Proper Motion Dec. does not indicate a stars true speed, change in true distance in light years, or change in position in three dimensional space, but just the observed motion on the two dimensional surface of the "sphere" from our viewpoint.
The apparent motions of the stars in the night sky are caused by the earth's rotation and orbit around the Sun, and the tiny effects of precession, and not related to proper motion. While the proper motion of a star is also an apparent motion, it is the result of the star's own motion in space. Proper Motion is simply a measure of how quickly a star appears to move in the sky based on it's own motion in space.
The observed speed of a stars Proper Motion is usually noted in units of arc seconds per year. A better way is to note arc seconds per year, for both Proper Motion RA and Proper Motion Dec., to define both the observed speed and the observed direction of drift on the celestial sphere . In this case be sure to note if the values are positive or negative. With this information, provided that you also account for precession, you can calculate a stars RA and Dec. over a period of years to determine the direction where the star would appear on the celestial sphere on any given date past or future.
Proper Motion RA and Proper Motion Dec. does not indicate a stars true speed, change in true distance in light years, or change in position in three dimensional space, but just the observed motion on the two dimensional surface of the "sphere" from our viewpoint.

Barnard's "Runaway" Star
The star with the greatest known proper motion is a dim (M 9.54) class M red dwarf variable star called Barnard's Star (Proxima Ophiuchi, V2500 Ophiuchi).
It is only 5.91 light years away (J2000) and moving unusually fast so that it appears to move 10.3 arc seconds per year.
[ RA: -0.798.71 as/year, Dec.: 10.33777 as/year ]
At this rate it takes 180 years to move the width of the diameter of the full Moon as seen from Earth. In 11,700 AD or so it will be at it's closest approach to our solar system, at about 3.8 light years. The simulation to the left closely approximates actual observations from 1985 to 2005, showing about 206 arc seconds of movement in 20 years.
Like Barnard's "Runaway" Star , the majority of the stars with unusually large proper motion tend to be too dim to see with the naked eye, but there are exceptions. The following table example lists a few of the brighter 1st magnitude stars that exhibit large proper motion.
The star with the greatest known proper motion is a dim (M 9.54) class M red dwarf variable star called Barnard's Star (Proxima Ophiuchi, V2500 Ophiuchi).
It is only 5.91 light years away (J2000) and moving unusually fast so that it appears to move 10.3 arc seconds per year.
[ RA: -0.798.71 as/year, Dec.: 10.33777 as/year ]
At this rate it takes 180 years to move the width of the diameter of the full Moon as seen from Earth. In 11,700 AD or so it will be at it's closest approach to our solar system, at about 3.8 light years. The simulation to the left closely approximates actual observations from 1985 to 2005, showing about 206 arc seconds of movement in 20 years.
Like Barnard's "Runaway" Star , the majority of the stars with unusually large proper motion tend to be too dim to see with the naked eye, but there are exceptions. The following table example lists a few of the brighter 1st magnitude stars that exhibit large proper motion.
| Star Name |
Identity | Magnitude | Spectral Class |
Distance ly |
RA | Dec | Proper Motion RA |
Proper Motion Dec |
|---|---|---|---|---|---|---|---|---|
| Sirius | Alpha Canis Majoris | -1.46 | A1Vm | 8.6 | 6h 45.148m | -16° 42.967' | -0.553 | -1.205 |
| Rigilkent | Alpha Centauri A | -0.01 | G2V | 4.44 | 14h 39.498m | -60° 50.117' | -3.642 | 0.699 |
| Rigilkent | Alpha Centauri B | 1.33 | K1V | 4.44 | 14h 39.602m | -60° 50.133' | -3.646 | 0.7 |
| Arcturus | Alpha Boötis | -0.05 | K1.5IIIFe-0.5 | 36.7 | 14h 15.662m | 19° 10.950' | -1.093 | -1.998 |
| Procyon | Alpha Canis Minoris | 0.38 | F5IV-V | 11.4 | 7h 39.302m | 5° 13.500' | -0.71 | -1.023 |
Although Barnard's Star is moving unusually fast, it is relevant to note
that Sirius, Alpha Centauri, Arcturus, Procyon, and Barnard's Star happen
to be some of our closest neighbors in the Milky Way Galaxy, and therefore
would be expected to exhibit larger angular motion in a shorter time period.
Imagine two cars, both in motion at say 65MPH, but one is very close, and the other is very far away. The one that is far away appears to move very slowly, while the closer one appears go by your location much more quickly. The apparent proper motions of the stars are affected by distance in the same way. Stars that are close might seem to move faster. Likewise, stars that are very far away exhibit very little motion of their own in a human lifetime .
Imagine two cars, both in motion at say 65MPH, but one is very close, and the other is very far away. The one that is far away appears to move very slowly, while the closer one appears go by your location much more quickly. The apparent proper motions of the stars are affected by distance in the same way. Stars that are close might seem to move faster. Likewise, stars that are very far away exhibit very little motion of their own in a human lifetime .
Magnitude (M) is the relative brightness of a particular star,
and magnitude numbers are used to indicate a stars brightness. As the magnitude numbers
get lower, the stars get brighter. Each decrease in magnitude number is roughly 2.5
times brighter than the next higher number.
Around 100 B.C. when the Greek astronomer Hipparchus divided stars into brightness classes, he called the brightest ones 1st magnitude. Those a little dimmer he designated 2nd magnitude, and so on down to the faintest ones he could see with the naked eye, 6th magnitude. When telescopes were invented in the 1600's, astronomers found that they could see even fainter stars, up to 9th magnitude. However, with the advent of the telescope, it also turned out that some of Hipparchus's 1st magnitude stars are brighter than others. In order to accommodate these stars, the scale now extends into negative numbers. Thus the brightest objects have a negative value, and as the numbers get larger or more positive, the stars get dimmer. Using this scale, and if the viewing conditions are excellent, the dimmest stars that you can generally see with the naked eye are about 5.5 to 6.0 magnitude. Binoculars will show stars as dim as 9th magnitude, and a 6" amateur telescope will go to about 13th. Large, sensitive telescopes used by professional astronomers can reach to about 29th magnitude, and the Hubbell Space Telescope so far can just reach 30th.
The brightest star at night, with a magnitude of -1.44 (negative 1.44), is Sirius (Alpha Canis Majoris), commonly called "the dog star". The fifth brightest star, with a magnitude of 0.03 (positive 0.03), is Vega (Alpha Lyrae). The planets in our own solar system have a magnitude number also, For example: Venus has a magnitude of -4.4 (negative 4.4). Since generally each decrease in magnitude number is roughly 2.5 times brighter than the next higher number, and since Sirius and the planet Venus are about 3 numbers apart, it follows that the planet Venus is about 15 times brighter than Sirius [ 2.53 = 15 ]. Of course our own Sun is a star also, and it has a magnitude of -26.8 making it about 12 billion times brighter than Sirius and 820 million times brighter than Venus.
When exploring, remember that while brightness or magnitude may be related to a stars distance from earth, it is not a positive indication of distance. Two stars that appear directly next to each other in the sky could actually be 100 or 10,000 light years apart in terms of distance from Earth. The point to understand is that because of differences in the types of stars, size, and spectral class, the brighter star may be the one that is farther away. Also remember that even in the best viewing conditions, all of the individual stars and clusters you can see with the naked eye are part of our own galaxy, the Milky Way. If you can see them at all with the naked eye, deep sky objects outside of our galaxy tend to look like smudges , and are best viewed with binoculars or a telescope.
Around 100 B.C. when the Greek astronomer Hipparchus divided stars into brightness classes, he called the brightest ones 1st magnitude. Those a little dimmer he designated 2nd magnitude, and so on down to the faintest ones he could see with the naked eye, 6th magnitude. When telescopes were invented in the 1600's, astronomers found that they could see even fainter stars, up to 9th magnitude. However, with the advent of the telescope, it also turned out that some of Hipparchus's 1st magnitude stars are brighter than others. In order to accommodate these stars, the scale now extends into negative numbers. Thus the brightest objects have a negative value, and as the numbers get larger or more positive, the stars get dimmer. Using this scale, and if the viewing conditions are excellent, the dimmest stars that you can generally see with the naked eye are about 5.5 to 6.0 magnitude. Binoculars will show stars as dim as 9th magnitude, and a 6" amateur telescope will go to about 13th. Large, sensitive telescopes used by professional astronomers can reach to about 29th magnitude, and the Hubbell Space Telescope so far can just reach 30th.
The brightest star at night, with a magnitude of -1.44 (negative 1.44), is Sirius (Alpha Canis Majoris), commonly called "the dog star". The fifth brightest star, with a magnitude of 0.03 (positive 0.03), is Vega (Alpha Lyrae). The planets in our own solar system have a magnitude number also, For example: Venus has a magnitude of -4.4 (negative 4.4). Since generally each decrease in magnitude number is roughly 2.5 times brighter than the next higher number, and since Sirius and the planet Venus are about 3 numbers apart, it follows that the planet Venus is about 15 times brighter than Sirius [ 2.53 = 15 ]. Of course our own Sun is a star also, and it has a magnitude of -26.8 making it about 12 billion times brighter than Sirius and 820 million times brighter than Venus.
When exploring, remember that while brightness or magnitude may be related to a stars distance from earth, it is not a positive indication of distance. Two stars that appear directly next to each other in the sky could actually be 100 or 10,000 light years apart in terms of distance from Earth. The point to understand is that because of differences in the types of stars, size, and spectral class, the brighter star may be the one that is farther away. Also remember that even in the best viewing conditions, all of the individual stars and clusters you can see with the naked eye are part of our own galaxy, the Milky Way. If you can see them at all with the naked eye, deep sky objects outside of our galaxy tend to look like smudges , and are best viewed with binoculars or a telescope.
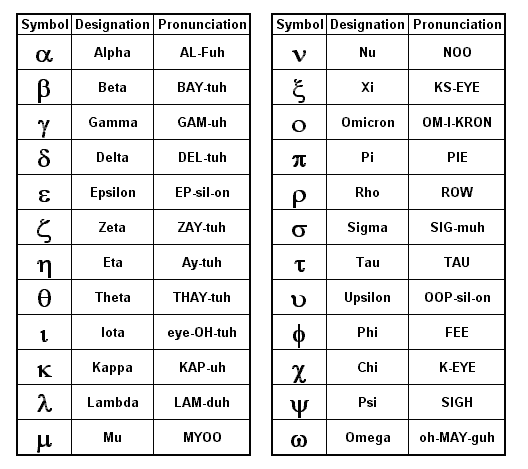
Identity is another way of identifying stars where stars are given lower case letters
of the Greek alphabet to indicate the brightness or magnitude
of the stars, along with the genitive name in Latin of the constellation they appear in.
These names are known as Bayer designations, and were introduced by Johan Bayer
in his star atlas, Uranometria, in 1603.
Because the brightest star in many constellations is designated as Alpha, many people logically assume that Bayer intended to put the stars in the order of their magnitude. If Bayer had the technology in 1603 to measure a stars magnitude accurately enough for that, he might have done it that way. Instead, he used the 6 traditional Hipparchus magnitude classes that astronomers were using at the time. What Bayer was able to do was arrange his catalog to list all 1st magnitude stars, then all 2nd magnitude and so on. Then he started at the head of the constellation figure and designated the first star nearest the head that was a 1st magnitude star as "Alpha". He then proceed towards the foot or tail of the figure and designated the next 1st magnitude star as "Beta", and so on until all of the 1st magnitude stars were designated. Then he started at the head again with the 2nd magnitude stars, and then the 3rd magnitude, and so on.
Orion is a good example of how Bayer's naming system works. He designated Alpha Orionis as the identity for Betelgeuse (0.5), the headmost 1st magnitude star in the constellation Orion. And although the 1st magnitude star Rigel (0.12) is actually the brightest star in Orion, it is at the right knee or foot of the figure so he designated it as Beta Orionis. Then he started at the head again with the second magnitude stars. Bellatrix (1.64, Gamma), Minitaka (2.23, Delta), Alnilam (1.7, Epsilon), Alnitak (2.05, Zeta), and so on to Saiph (2.06, Kappa) at the left knee or foot. As you can see, they are not in exact order of magnitide. Then back to the head again with the third magnitude stars starting with Meissa (3.54, Lambda), etc. Of these listed, only Bellatrix, the third brightest star in the constellation Orion was lucky enough to draw the corresponding alphabet sequence (Gamma) according to the actual magnitude of the star. Maybe we should count Bellatrix as one of our lucky stars.
The Bayer system is more useful way of naming stars because it describes both the constellation where the star is, as well as which specific star. In addition, because for historical and cultural reasons there are often different names for the same star, it provides a simple but common frame of reference. For example, Beta Orionis is commonly known to most of us as Rigel from the Arabic word Ar-Rijl, meaning "The Foot", but it also has been called Algebar, from the Arabic word Al-jabbar meaning "The Giant". In star catalogs you may find both Rigel and Algebar listed as Beta Orionis. The does not mean that there are two beta stars in the constellation Orion, but that there are two names for the same star. If you compare the RA, Dec, and Spectral Class, you should see that they are the same. Referring to this star's identity instead of it's name is more clear because no matter what name it had in the past, or may have tomorrow, it will always be Beta Orionis.
Still, there are some cases where you may find two or more different stars in the same constellation with the same Bayer designation. An example of this is Alpha Centauri, where you have a triple star system consisting of two main stars, Alpha Centauri "A" and "B" orbiting one another elliptically every 80 years to form a binary star. To the naked eye, the very bright yellow dwarf "A", and the orange dwarf "B", are too close to be able to resolve as separate stars, and so are perceived together as Rigilkent, the fourth brightest star in the night sky. The third alpha star is Proxima, a dimmer red dwarf which which possibly may be in orbit about "A" and "B" with a period of about 500,000 years or more, and is sometimes called Alpha Centauri "C".
Well known stars have many designations. For example: Vega is the same as Alpha Lyrae, SAO 67174, HD 172167, etc., depending on which reference is used. Many stars do not have names or Bayer designations. They may be given numbers or letters similar to Bayer designations such as 3 Sagittarii, S Leporis, 35 Draconis, EE Pegasi, etc. Some stars just have catalog numbers such as SAO 132301.
Bayer designations are always lower case as shown in the following table.
Because the brightest star in many constellations is designated as Alpha, many people logically assume that Bayer intended to put the stars in the order of their magnitude. If Bayer had the technology in 1603 to measure a stars magnitude accurately enough for that, he might have done it that way. Instead, he used the 6 traditional Hipparchus magnitude classes that astronomers were using at the time. What Bayer was able to do was arrange his catalog to list all 1st magnitude stars, then all 2nd magnitude and so on. Then he started at the head of the constellation figure and designated the first star nearest the head that was a 1st magnitude star as "Alpha". He then proceed towards the foot or tail of the figure and designated the next 1st magnitude star as "Beta", and so on until all of the 1st magnitude stars were designated. Then he started at the head again with the 2nd magnitude stars, and then the 3rd magnitude, and so on.
Orion is a good example of how Bayer's naming system works. He designated Alpha Orionis as the identity for Betelgeuse (0.5), the headmost 1st magnitude star in the constellation Orion. And although the 1st magnitude star Rigel (0.12) is actually the brightest star in Orion, it is at the right knee or foot of the figure so he designated it as Beta Orionis. Then he started at the head again with the second magnitude stars. Bellatrix (1.64, Gamma), Minitaka (2.23, Delta), Alnilam (1.7, Epsilon), Alnitak (2.05, Zeta), and so on to Saiph (2.06, Kappa) at the left knee or foot. As you can see, they are not in exact order of magnitide. Then back to the head again with the third magnitude stars starting with Meissa (3.54, Lambda), etc. Of these listed, only Bellatrix, the third brightest star in the constellation Orion was lucky enough to draw the corresponding alphabet sequence (Gamma) according to the actual magnitude of the star. Maybe we should count Bellatrix as one of our lucky stars.
The Bayer system is more useful way of naming stars because it describes both the constellation where the star is, as well as which specific star. In addition, because for historical and cultural reasons there are often different names for the same star, it provides a simple but common frame of reference. For example, Beta Orionis is commonly known to most of us as Rigel from the Arabic word Ar-Rijl, meaning "The Foot", but it also has been called Algebar, from the Arabic word Al-jabbar meaning "The Giant". In star catalogs you may find both Rigel and Algebar listed as Beta Orionis. The does not mean that there are two beta stars in the constellation Orion, but that there are two names for the same star. If you compare the RA, Dec, and Spectral Class, you should see that they are the same. Referring to this star's identity instead of it's name is more clear because no matter what name it had in the past, or may have tomorrow, it will always be Beta Orionis.
Still, there are some cases where you may find two or more different stars in the same constellation with the same Bayer designation. An example of this is Alpha Centauri, where you have a triple star system consisting of two main stars, Alpha Centauri "A" and "B" orbiting one another elliptically every 80 years to form a binary star. To the naked eye, the very bright yellow dwarf "A", and the orange dwarf "B", are too close to be able to resolve as separate stars, and so are perceived together as Rigilkent, the fourth brightest star in the night sky. The third alpha star is Proxima, a dimmer red dwarf which which possibly may be in orbit about "A" and "B" with a period of about 500,000 years or more, and is sometimes called Alpha Centauri "C".
Well known stars have many designations. For example: Vega is the same as Alpha Lyrae, SAO 67174, HD 172167, etc., depending on which reference is used. Many stars do not have names or Bayer designations. They may be given numbers or letters similar to Bayer designations such as 3 Sagittarii, S Leporis, 35 Draconis, EE Pegasi, etc. Some stars just have catalog numbers such as SAO 132301.
Bayer designations are always lower case as shown in the following table.
After Omega, you have to start over with Alpha2, Beta2, etc. Of course the Bayer system is not without it's issues; the key issue
being that there are only 24 letters in the Greek alphabet and possibly
300 billion stars in our Milky Way Galaxy. Still, it works very well for
the brightest stars that form the basic shape of a constellation that we
are most likely to be familiar with.
Kelvin is a unit of temperature measured with respect to absolute zero, the temperature
where molecular motion stops. The symbol for kelvin temperature is K, and
unlike °C or °F is not preceded with the word degrees or the degree symbol.
0.0 K = -273.15 °C, where K = °C + 273.15
0.0 °C = 273.15 K, where °C = K - 273.15
0.0 K = -459.67 °F, where K = (°F + 459.67) / 1.8
0.0 °F = 255.37 K, where °F = (K x 1.8) - 459.67
5800 K = 5,526.8 °C = 9,980.3 °F = Class G2 = the Sun
0.0 K = -273.15 °C, where K = °C + 273.15
0.0 °C = 273.15 K, where °C = K - 273.15
0.0 K = -459.67 °F, where K = (°F + 459.67) / 1.8
0.0 °F = 255.37 K, where °F = (K x 1.8) - 459.67
5800 K = 5,526.8 °C = 9,980.3 °F = Class G2 = the Sun
Spectral Class is a method of classifying stars based on
their color. The color of a star depends on its surface temperature, with the hottest stars
having a bluish to white tint, the cooler stars having a yellow to red tint, and the coldest stars
radiating in the deep red to invisible infra-red range. Stars can range in temperature from
"cold" at only 2000 K (kelvin) for an extreme red giant, to 100,000 K
for a star inside a planetary nebula, to over a million K for a neutron star.
First of all, they are given a letter code to indicate their MKK class. Next a decimalized number from 0.00 to 9.99 to further subdivide the classes, with 0.00 being at the hot end of the class and 9.99 being at the cool end of the class. And finally they receive a Roman numeral to indicate their luminosity class, which can also be subdivided with a lower case letter. A class IIa is more luminous than a class IIb, and so on. Double or Binary Stars might be noted with a plus sign as in for example A2III+A4IV.
Our own star, the Sun, is a medium class yellow star exhibiting weaker hydrogen spectral bands, bands of ionized metals, and bands of neutral metals, and has a surface temperature of 5800 K, so it is class G2. That means that while the core is much hotter, the average surface temperature of the Sun is a relatively cool 10,000° F. It is interesting to note that one of the nearest stars, Alpha Centauri A is very much like our own Sun.
The following tables explain the differences in the different MKK Classes and Luminosity Classes. Where star spectral data is presented in my object catalog, I used the same color code scheme to highlight the spectral class of each star listed.
First of all, they are given a letter code to indicate their MKK class. Next a decimalized number from 0.00 to 9.99 to further subdivide the classes, with 0.00 being at the hot end of the class and 9.99 being at the cool end of the class. And finally they receive a Roman numeral to indicate their luminosity class, which can also be subdivided with a lower case letter. A class IIa is more luminous than a class IIb, and so on. Double or Binary Stars might be noted with a plus sign as in for example A2III+A4IV.
Our own star, the Sun, is a medium class yellow star exhibiting weaker hydrogen spectral bands, bands of ionized metals, and bands of neutral metals, and has a surface temperature of 5800 K, so it is class G2. That means that while the core is much hotter, the average surface temperature of the Sun is a relatively cool 10,000° F. It is interesting to note that one of the nearest stars, Alpha Centauri A is very much like our own Sun.
The following tables explain the differences in the different MKK Classes and Luminosity Classes. Where star spectral data is presented in my object catalog, I used the same color code scheme to highlight the spectral class of each star listed.
| MKK Class |
Spectrum | Color | Temperature Range |
|---|---|---|---|
| O | Ionized and Neutral Helium Bands Weakened Hydrogen Bands |
Blue | 31,000°-49,000° K |
| B | Neutral Helium Bands Stronger Hydrogen Bands |
Blue-White | 10,000°-31,000° K |
| A | Strong Hydrogen Bands Ionized Metals |
White | 7400°-10,000° K |
| F | Weaker Hydrogen Bands Ionized Metals |
Yellow-White | 6000°-7400° K |
| G | Still Weaker Hydrogen Bands Ionized and Neutral Metals |
Yellow | 5300°-6000° K |
| K | Weak Hydrogen Bands Neutral Metals |
Orange | 3900°-5300° K |
| M | Little or No Hydrogen Bands Neutral Metals, Molecules |
Red | 2200°-3900° K |
| L | No Hydrogen Bands Metallic Hydrides, Alkali Metals |
Red-Infrared | 1200°-2200° K |
| T | Methane Bands | Infrared | Under 1200 °K |
| Luminosity Class |
Type |
|---|---|
| 0 and Ia | HyperGiant |
| I | SuperGiant |
| II | BrightGiant |
| III | Giant |
| IV | SubGiant |
| V | Dwarf |
Sidereal Time is astronomical time or star time, and is slightly different from Solar Time. In astronomy, in order to
know exactly when a particular star or constellation will appear overhead,
we are concerned with how long it takes the Earth to spin exactly 360°
with respect to the "fixed" stars. One revolution of the earth is called a Sidereal Day. The Earth takes approximately 23 hours and 56 Minutes to complete one full 360° revolution (23.9345 hours).
Solar time is a little different in that it is concerned with how long it takes the sun to travel 360° around in the sky due to Earth's rotation. This is called a Solar Day. We arbitrarily divide each solar day into 24 equal parts so that starting at noon with the Sun directly overhead, it appears to take exactly 24 hours for the Sun to be directly overhead at noon the next day. The time reference we all use is based on the 24 hour Solar Day, so it is very natural for non-astronomers to mistakenly believe that 24 hours is the same as one revolution of the Earth.
Solar time is a little different in that it is concerned with how long it takes the sun to travel 360° around in the sky due to Earth's rotation. This is called a Solar Day. We arbitrarily divide each solar day into 24 equal parts so that starting at noon with the Sun directly overhead, it appears to take exactly 24 hours for the Sun to be directly overhead at noon the next day. The time reference we all use is based on the 24 hour Solar Day, so it is very natural for non-astronomers to mistakenly believe that 24 hours is the same as one revolution of the Earth.
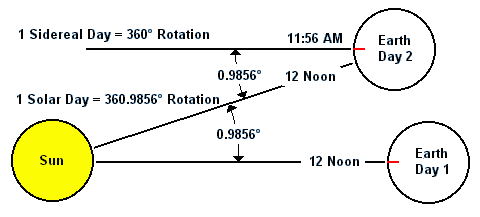
A Sidereal Day and a Solar Day are NOT the same. As this exaggerated drawing
shows, the difference between a sidereal day and a solar day is a matter
of about 1 extra degree in the Earth's rotation. Because the Earth is in
orbit around the Sun, it actually has to physically rotate almost 361 degrees
to make the Sun look like it has traveled 360 degrees around the Sky.
The rotating Earth moves about one degree per day [ 360° / 365.25 Days per Year = 0.9856° per Day ] along its yearly orbit around the Sun.
If you start on day 1 at noon, and after the earth has rotated a full 360° in relation to the
stars to get to day 2, the solar time will be about 11:56 AM, or 4 minutes short
of noon because the Earth is now in a different position with respect to
the Sun.
The added variable of the Earth's orbit around the sun combined with the way we tell time, means that a star that is directly overhead at 8:00 PM local solar time tonight, will be about one degree West at 8:00 PM the following night, and 2 degrees West at 8:00 PM the next night, and so on until 6 months from now it is on the day side of the earth at 8:00 PM, and finally a year from now it is directly overhead again at 8:00 PM. In order to see the stars on the other side of the sun, we have to wait until the earth gets on the other side of the sun.
Actually, this works out great, because if the Earth wasn't in orbit around the Sun, we would see the same stars every night of the year. There wouldn't be summer stars and winter stars. On the other hand, the Earth's yearly orbit means that your watch or clock cannot tell you which stars are in the sky or when a particular star might be visible.
To make things easy, astronomers use Local Apparent Sidereal Time (LST) adjusted to the the same right ascension (RA) on the celestial sphere that is currently crossing the local meridian (Local North/South Line). In other words, the time when an object on the celestial sphere is directly overhead at its highest point in the sky, or culmination, as viewed from your specific local longitude on earth. Once you know what the Local Sidereal Time is, you always know exactly what object is on your meridian, because the Local Sidereal Time is the same as the RA of the object. In other words, local star time.
For example: Orion has an RA of about 5h 34m, so when the Local Sidereal Time is 05:34:00, Orion is directly on your North/South Line. Of course depending on the time of year, it might also be 9:00 AM Local Solar Time and you can't see any stars; or depending on your local latitude Orion may be below the horizon, but at least you always know where you are in relation to the stars on the celestial sphere.
Local Sidereal Time will also allow you to figure out how many degrees East or West of your local meridian you need to look to find an object. Each 15° East of your meridian corresponds to +1h RA, and each 15° West of your meridian is -1h RA. So when your local sidereal clock displays 08:00:00, and if you wanted to find the Constellation Leo which is at RA 10:00:00, you would find Leo +2h or 30° East of the local meridian.
To keep the Sun out of the equation and keep track of Local Sidereal Time, astronomers use a special sidereal clock that runs about 4 minutes fast each day (1 sec every 6 min). In fact, there are nice quartz analog Sidereal wall clocks that you can buy. You just set it to Local Sidereal Time and it will tell you which constellation is on your meridian and which star charts to use through the year.
By far the easiest way is to use any number of computer programs and Javascript calculators that convert UTC from your computer's clock into Greenwich Mean Sidereal Time, and then offset it to display Local Sidereal Time. The calculations are accurate to within one or two seconds per year, which is probably more accurate than your computer clock. For scripts, all you need is a web browser and your local longitude value. To see how this works, there is a free sidereal clock javascript with source code available in my software section.
Some other ways to find your current local Sidereal Time:
1. Look it up on a web site such as the U.S. Naval Observatory. http://tycho.usno.navy.mil/sidereal.html Enter your exact longitude, and it returns your current Local Sidereal Time.
2. Local Sidereal Time is always equal to the right ascension of any star or constellation currently on the observer's meridian (North/South Line). It is just a matter of how accurately you are able to line up the star with the meridian. When you find yourself in the field without your fancy computer telescope program to show you the current sky view, just set your watch to the RA of the object directly on your local meridian, and it will be accurate enough for a couple of nights viewing. It is also a very handy trick if you don't know your exact longitude or time zone.
3. The sidereal day begins exactly at 0 hours every year when the vernal equinox crosses the celestial meridian. On or about March 21, the sun is located at the vernal equinox, and will be on your local meridian at noon solar time. By definition, the local sidereal time on March 21 is 0h at noon, local mean time (Where you are). When you get stuck on a deserted island, you can use this fact with just your watch and compass to quickly estimate what day of the year it is. If you set your watch correctly to the RA of a known object on your North/South line the night before, you can figure out the local sidereal time when the sun is on your meridian the next day. Then for example: If the local sidereal time when the Sun's shadow runs North and South is 02:08, that is roughly 32° hour angle past the vernal equinox [ 02:08 = 15° per hour + 1° for each 4 minutes = 32° ]. And since each degree difference in hour angle is approximately one solar day, that makes it roughly 32 days after March 21, or about April 22. More exactly, noon, April 21 [ 32° x 0.9856° per day = 31.53 days ]. It may not get you rescued, but at least it will give you something to do while you wait.
4. Sidereal time can also be found with an astrolabe. The astrolabe is a very ancient astronomical computer for solving problems relating to time and the position of the Sun and stars in the sky. Modern astrolabes made of plastic can be very inexpensive. The key issue is that they are calibrated to work only in your exact location, and are not very accurate past 150 miles radius of the location they were made for. Local sidereal time is the hour angle of the vernal equinox at Aries 0° (the so-called, "First Point of Aries"). To find the current local sidereal time, the rete is rotated to the current position of the ecliptic and the local sidereal time is read directly from the position of the vernal equinox. (Just for fun)
The added variable of the Earth's orbit around the sun combined with the way we tell time, means that a star that is directly overhead at 8:00 PM local solar time tonight, will be about one degree West at 8:00 PM the following night, and 2 degrees West at 8:00 PM the next night, and so on until 6 months from now it is on the day side of the earth at 8:00 PM, and finally a year from now it is directly overhead again at 8:00 PM. In order to see the stars on the other side of the sun, we have to wait until the earth gets on the other side of the sun.
Actually, this works out great, because if the Earth wasn't in orbit around the Sun, we would see the same stars every night of the year. There wouldn't be summer stars and winter stars. On the other hand, the Earth's yearly orbit means that your watch or clock cannot tell you which stars are in the sky or when a particular star might be visible.
To make things easy, astronomers use Local Apparent Sidereal Time (LST) adjusted to the the same right ascension (RA) on the celestial sphere that is currently crossing the local meridian (Local North/South Line). In other words, the time when an object on the celestial sphere is directly overhead at its highest point in the sky, or culmination, as viewed from your specific local longitude on earth. Once you know what the Local Sidereal Time is, you always know exactly what object is on your meridian, because the Local Sidereal Time is the same as the RA of the object. In other words, local star time.
For example: Orion has an RA of about 5h 34m, so when the Local Sidereal Time is 05:34:00, Orion is directly on your North/South Line. Of course depending on the time of year, it might also be 9:00 AM Local Solar Time and you can't see any stars; or depending on your local latitude Orion may be below the horizon, but at least you always know where you are in relation to the stars on the celestial sphere.
Local Sidereal Time will also allow you to figure out how many degrees East or West of your local meridian you need to look to find an object. Each 15° East of your meridian corresponds to +1h RA, and each 15° West of your meridian is -1h RA. So when your local sidereal clock displays 08:00:00, and if you wanted to find the Constellation Leo which is at RA 10:00:00, you would find Leo +2h or 30° East of the local meridian.
To keep the Sun out of the equation and keep track of Local Sidereal Time, astronomers use a special sidereal clock that runs about 4 minutes fast each day (1 sec every 6 min). In fact, there are nice quartz analog Sidereal wall clocks that you can buy. You just set it to Local Sidereal Time and it will tell you which constellation is on your meridian and which star charts to use through the year.
By far the easiest way is to use any number of computer programs and Javascript calculators that convert UTC from your computer's clock into Greenwich Mean Sidereal Time, and then offset it to display Local Sidereal Time. The calculations are accurate to within one or two seconds per year, which is probably more accurate than your computer clock. For scripts, all you need is a web browser and your local longitude value. To see how this works, there is a free sidereal clock javascript with source code available in my software section.
Some other ways to find your current local Sidereal Time:
1. Look it up on a web site such as the U.S. Naval Observatory. http://tycho.usno.navy.mil/sidereal.html Enter your exact longitude, and it returns your current Local Sidereal Time.
2. Local Sidereal Time is always equal to the right ascension of any star or constellation currently on the observer's meridian (North/South Line). It is just a matter of how accurately you are able to line up the star with the meridian. When you find yourself in the field without your fancy computer telescope program to show you the current sky view, just set your watch to the RA of the object directly on your local meridian, and it will be accurate enough for a couple of nights viewing. It is also a very handy trick if you don't know your exact longitude or time zone.
3. The sidereal day begins exactly at 0 hours every year when the vernal equinox crosses the celestial meridian. On or about March 21, the sun is located at the vernal equinox, and will be on your local meridian at noon solar time. By definition, the local sidereal time on March 21 is 0h at noon, local mean time (Where you are). When you get stuck on a deserted island, you can use this fact with just your watch and compass to quickly estimate what day of the year it is. If you set your watch correctly to the RA of a known object on your North/South line the night before, you can figure out the local sidereal time when the sun is on your meridian the next day. Then for example: If the local sidereal time when the Sun's shadow runs North and South is 02:08, that is roughly 32° hour angle past the vernal equinox [ 02:08 = 15° per hour + 1° for each 4 minutes = 32° ]. And since each degree difference in hour angle is approximately one solar day, that makes it roughly 32 days after March 21, or about April 22. More exactly, noon, April 21 [ 32° x 0.9856° per day = 31.53 days ]. It may not get you rescued, but at least it will give you something to do while you wait.
4. Sidereal time can also be found with an astrolabe. The astrolabe is a very ancient astronomical computer for solving problems relating to time and the position of the Sun and stars in the sky. Modern astrolabes made of plastic can be very inexpensive. The key issue is that they are calibrated to work only in your exact location, and are not very accurate past 150 miles radius of the location they were made for. Local sidereal time is the hour angle of the vernal equinox at Aries 0° (the so-called, "First Point of Aries"). To find the current local sidereal time, the rete is rotated to the current position of the ecliptic and the local sidereal time is read directly from the position of the vernal equinox. (Just for fun)
Universal Time (UT) or (ZULU), was long known as Greenwich Mean Time (GMT). Since quoting
a time to another astronomer depends on where you happen to be, astronomers
need a standard time reference that is not dependant on location or local
time zone. This standard reference is UT, for Universal Time zone. The
Universal Time zone is 0° longitude, which is by definition, that of a
line engraved in a brass plate in the floor of the Old Royal Observatory
at Greenwich, England. UT is always stated in the 24-hour system, where
noon is called 12:00, 1 p.m. is 13:00, 2 p.m. is 14:00, and so on. Midnight
is called 0:00.
If you live in the US, the following table will help you to convert UT to local time, for both standard and daylight time. To convert from UT without using the table, subtract the number of hours in the table header for your time zone. If the result is negative, add 24 hours but subtract one day. For example: to convert Sat, Feb 11, 2009 @ 1:32 UT to Pacific Standard Time, subtract 8 hours, which gives you -7, plus 24, minus one day, which gives you Friday, Feb 10, 2009 @ 17:32 PST. For convenience, the times shown in red indicate that you use the previous day, otherwise it is the same day.
When converting, you will have to remember that starting in 2007, most of the United States and Canada observe Daylight Saving Time from the second Sunday in March to the first Sunday in November, almost two-thirds of the year.
If you live in the US, the following table will help you to convert UT to local time, for both standard and daylight time. To convert from UT without using the table, subtract the number of hours in the table header for your time zone. If the result is negative, add 24 hours but subtract one day. For example: to convert Sat, Feb 11, 2009 @ 1:32 UT to Pacific Standard Time, subtract 8 hours, which gives you -7, plus 24, minus one day, which gives you Friday, Feb 10, 2009 @ 17:32 PST. For convenience, the times shown in red indicate that you use the previous day, otherwise it is the same day.
When converting, you will have to remember that starting in 2007, most of the United States and Canada observe Daylight Saving Time from the second Sunday in March to the first Sunday in November, almost two-thirds of the year.
| Time Zones |
EST | EDT | CST | CDT | MST | MDT | PST | PDT | Time Zones |
EST | EDT | CST | CDT | MST | MDT | PST | PDT | |
| UT (GMT) |
-5h | -4h | -6h | -5h | -7h | -6h | -8h | -7h | UT (GMT) |
-5h | -4h | -6h | -5h | -7h | -6h | -8h | -7h | |
| 0h | 19h | 20h | 18h | 19h | 17h | 18h | 16h | 17h | 12h | 7h | 8h | 6h | 7h | 5h | 6h | 4h | 5h | |
| 1h | 20h | 21h | 19h | 20h | 18h | 19h | 17h | 18h | 13h | 8h | 9h | 7h | 8h | 6h | 7h | 5h | 6h | |
| 2h | 21h | 22h | 20h | 21h | 19h | 20h | 18h | 19h | 14h | 9h | 10h | 8h | 9h | 7h | 8h | 6h | 7h | |
| 3h | 22h | 23h | 21h | 22h | 20h | 21h | 19h | 20h | 15h | 10h | 11h | 9h | 10h | 8h | 9h | 7h | 8h | |
| 4h | 23h | 0h | 22h | 23h | 21h | 22h | 20h | 21h | 16h | 11h | 12h | 10h | 11h | 9h | 10h | 8h | 9h | |
| 5h | 0h | 1h | 23h | 0h | 22h | 23h | 21h | 22h | 17h | 12h | 13h | 11h | 12h | 10h | 11h | 9h | 10h | |
| 6h | 1h | 2h | 0h | 1h | 23h | 0h | 22h | 23h | 18h | 13h | 14h | 12h | 13h | 11h | 12h | 10h | 11h | |
| 7h | 2h | 3h | 1h | 2h | 0h | 1h | 23h | 0h | 19h | 14h | 15h | 13h | 14h | 12h | 13h | 11h | 12h | |
| 8h | 3h | 4h | 2h | 3h | 1h | 2h | 0h | 1h | 20h | 15h | 16h | 14h | 15h | 13h | 14h | 12h | 13h | |
| 9h | 4h | 5h | 3h | 4h | 2h | 3h | 1h | 2h | 21h | 16h | 17h | 15h | 16h | 14h | 15h | 13h | 14h | |
| 10h | 5h | 6h | 4h | 5h | 3h | 4h | 2h | 3h | 22h | 17h | 18h | 16h | 17h | 15h | 16h | 14h | 15h | |
| 11h | 6h | 7h | 5h | 6h | 4h | 5h | 3h | 4h | 23h | 18h | 19h | 17h | 18h | 16h | 17h | 15h | 16h |
Light Years (ly) is the unit of measurement used to describe how far
a star is from earth, or from another star. It is the distance light travels in one year.
The "speed of light" ("c") is 300,000 kilometers per second (186,000 miles per second)
or just under 670 million miles per hour! That makes one light year about 9.454 trillion kilometers,
5.8746 trillion miles, or 63,197.79 Astronomical Units (AU).
One AU is the average distance between the Earth and the Sun which is about 92.9558 million miles, making the sun about 8.3 Light Minutes from earth. Even at the speed of light, it takes over 8 minutes for the light from the Sun to reach Earth.
It takes about 100,000 years for the light from the Sun to reach the other side of our own galaxy, the Milky Way.
In the Milky Way, the closest star system beyond our own solar system is Rigilkent (Alpha Centauri), at 4.2 to 4.4 light years. The brightest object outside of our own solar system is Sirius (Alpha Canis Majoris), which is also one of our closest neighbors at 8.6 light years.
The nearest known galaxy beyond our own Milky Way Galaxy is the Canis Major Dwarf Galaxy, and is about 25,000 light years away from our solar system and 42,000 light years from the center of the Milky Way. Currently it is believed that the Canis Major Dwarf Galaxy has been, and still is colliding with the Milky Way, and has already contributed to about 1% of the mass of our galaxy. The closest large spiral galaxy similar to ours is M31, the Andromeda Galaxy, believed to be over two million light years away.
Some of the farthest and faintest objects we can see with the Hubbell Space Telescope may be over 12 billion light years away. Just as the light from the Sun left the Sun over eight minutes ago, the light we see today with Hubbell may have left these distant objects 12 billion years ago.
One AU is the average distance between the Earth and the Sun which is about 92.9558 million miles, making the sun about 8.3 Light Minutes from earth. Even at the speed of light, it takes over 8 minutes for the light from the Sun to reach Earth.
It takes about 100,000 years for the light from the Sun to reach the other side of our own galaxy, the Milky Way.
In the Milky Way, the closest star system beyond our own solar system is Rigilkent (Alpha Centauri), at 4.2 to 4.4 light years. The brightest object outside of our own solar system is Sirius (Alpha Canis Majoris), which is also one of our closest neighbors at 8.6 light years.
The nearest known galaxy beyond our own Milky Way Galaxy is the Canis Major Dwarf Galaxy, and is about 25,000 light years away from our solar system and 42,000 light years from the center of the Milky Way. Currently it is believed that the Canis Major Dwarf Galaxy has been, and still is colliding with the Milky Way, and has already contributed to about 1% of the mass of our galaxy. The closest large spiral galaxy similar to ours is M31, the Andromeda Galaxy, believed to be over two million light years away.
Some of the farthest and faintest objects we can see with the Hubbell Space Telescope may be over 12 billion light years away. Just as the light from the Sun left the Sun over eight minutes ago, the light we see today with Hubbell may have left these distant objects 12 billion years ago.
| Proxima Centauri (Alpha Centauri C) | 4.22 ly | Ross 128 (FI Virginis) | 10.8 ly | |
| Rigilkent (Alpha Centauri A & B) | 4.44 ly | Procyon (Alpha Canis Minoris) | 11.4 ly | |
| Barnard's Star (Proxima Ophiuchi) | 5.91 ly | (Tau Ceti) | 11.9 ly | |
| Wolf 359 (CN Leonis) | 7.7 ly | Altair (Alpha Aquilae) | 16.3 ly | |
| Sirius A & B (Alpha Canis Majoris) | 8.6 ly | Achird (Eta Cassiopeiae) | 19 ly | |
| (Epsilon Eridani) | 10.7 ly |
For more on constellations, stars, meteors, etc., check out...
Indy's Object Catalog - Catalog Index
Indy's Object Catalog - Catalog Index